Aug 2024
Deep Neural Networks for Predicting Critical Points of Fluid Mixtures
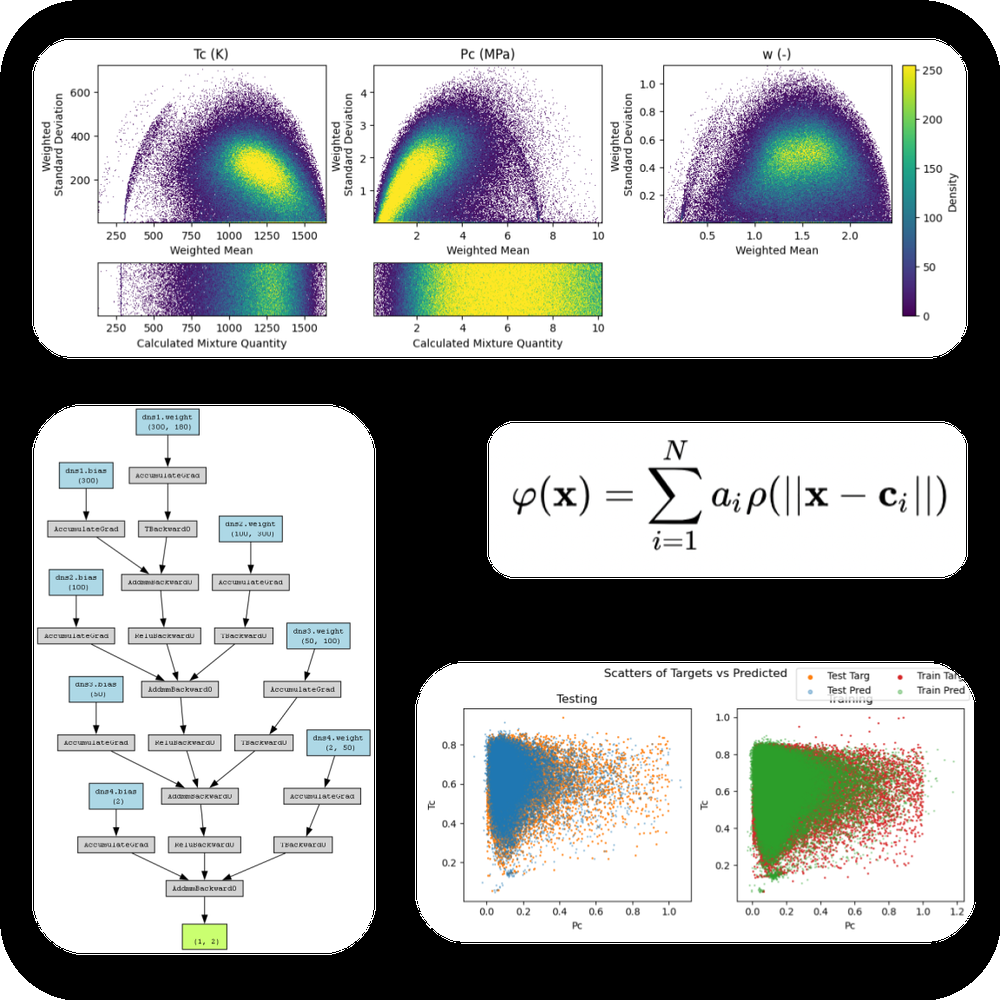
Top: plots showing the distribution of the training data. Middle: equation for a radial basis function. Bottom left: diagram of the model architecture. Bottom right: Plots comparing the distribution of predicted data in training and in testing.
My work as an undergraduate researcher in the summer of 2024 was centered around the development of a deep neural network (DNN) model capable of approximating the calculation of critical points for multi-phase fluid mixtures.
The reason for this work was to improve the performance of critical point calculations for fluid mixtures. Conventionally, these calculations are based on root-finding algorithms which are slow and unreliable. However, neural networks have the potential to proxy (replace) these calculations, or provide better initial guesses for conventional algorithms.
Critical points in multi-phase fluid mixtures represent conditions at which the distinct liquid and vapor phases of a mixture become indistinguishable. Knowing these points is essential for designing chemical processes, predicting phase behavior, and ensuring safe and efficient operation in many chemical and petroleum engineering situations.
During this project, I:
Learned underlying thermodynamics theory to better understand the problem I was trying to solve.
Scraped, cleaned, and processed data from multiple empirical sources (totalling over 500,000 values) using pandas and numpy.
Developed, trained, and evaluated DNN models with various architectures, and coded my own radial basis (RBF) activation function.
Analyzed results and made decisions on which models seemed most promising.
This project was foundational for my understanding of what is required to develop neural networks that actually work.
Plots showing different views of the same data in three-dimensional space. The plots axes are critical specific volume (vc), critical pressure (Pc), and critical temperature (Tc), which describe the conditions at which a fluid becomes critical.